A mathematical model for managing the number of stray dogs in big cities
A mathematical model for managing the number of stray dogs in big cities
Abstract
A mathematical model of stray dog population management is an important tool for effective population control in urban environments. This model integrates various parameters including breeding rates, mortality and migration rates, and the effectiveness of sterilization programmes. The model is based on a logistic equation that accounts for the interaction of various factors that influence the population dynamics of stray dogs. The model provides the ability to predict changes in population size in response to various interventions, such as sterilization programmes or environmental changes. Its generation requires the collection and analysis of data on various aspects of stray dog life, which allows the model to be accurately adapted to the specific conditions of the city. The mathematical model becomes a key tool in developing sustainable stray dog population management strategies to ensure the safety of urban residents and improve animal welfare.
1. Введение
Вопрос управления численностью бродячих собак является одной из актуальных проблем в крупных городах по всему миру. Нарастающая численность бездомных животных влечет за собой ряд социальных, экологических и здравоохранительных проблем. Одним из эффективных методов решения этой проблемы является стерилизация бродячих собак, которая помогает контролировать их популяцию без использования насильственных методов .
Математические модели стали незаменимым инструментом в управлении популяциями животных. Создание такой модели для управления численностью бродячих собак в крупных городах требует анализа множества факторов, таких как скорость размножения, смертность, степень миграции, и, конечно, эффективность стерилизации .
Цель данного исследования заключается в разработке математической модели, предназначенной для анализа и управления численностью бродячих собак в крупных городах с использованием программы стерилизации. Основной фокус направлен на создание устойчивого и эффективного подхода к контролю популяции бродячих собак, минимизации социальных и здравоохранительных проблем, а также обеспечения благоприятной среды для городского населения и животных.
2. Методы и принципы исследования
Для разработки математической модели управления численностью бродячих собак использовались данные о текущей популяции, ее структуре и поведенческих особенностях. Литературный обзор по экологии и поведению бродячих собак предоставил необходимые параметры для модели. Информация о проведенных программах стерилизации была использована для внедрения коэффициента эффективности стерилизации в модель , , .
Создание модели включало использование логистического уравнения для описания размножения бродячих собак и интеграцию параметров, таких как коэффициенты смертности, миграции и эффективности стерилизации. Модель адаптировалась к местным условиям на основе данных о численности и поведении бродячих собак в городе , .
Процесс калибровки модели включал итеративную коррекцию параметров с использованием фактических данных о популяции бродячих собак. Модель проверялась на соответствие реальным трендам в изменении численности популяции.
Для валидации модели использовались независимые данные, если таковые были доступны. Прогнозы модели сравнивались с фактическими изменениями в численности популяции с течением времени .
Оценка воздействия интервенций проводилась через сценарный анализ, который оценивал эффективность различных программ управления популяцией, включая стерилизацию и другие меры. Влияние изменений в параметрах модели на динамику популяции также учитывалось.
3. Основные результаты
Одной из ключевых переменных в такой модели является скорость размножения собак. Эта переменная зависит от множества факторов, включая возраст первого размножения, частоту размножения в год, и среднее количество потомства. Учет этих факторов позволяет создать более точную модель динамики популяции бродячих собак.
Смертность также играет важную роль в модели. Естественная смертность, болезни и травмы сокращают численность популяции. Эти факторы следует включить в модель, чтобы учесть реальные условия среды обитания бродячих собак .
Степень миграции – еще один важный аспект. Бродячие собаки могут перемещаться в пределах города, что влияет на их численность в различных районах. Моделирование миграции позволяет предсказать, как изменения в одном районе могут влиять на другие .
Эффективность программы стерилизации является ключевым фактором в контроле популяции бродячих собак. Это включает в себя не только сам процесс стерилизации, но и обеспечение доступности услуг, обучение общества и сотрудничество с волонтерами и местными организациями , .
Математическая модель может предоставить инструмент для оптимизации программ управления численностью бродячих собак. Интеграция данных, полученных из реальных наблюдений, позволяет улучшить точность и прогнозы модели .
Математическая модель управления численностью бродячих собак при стерилизации в крупных городах представляет собой систему уравнений, описывающих динамику популяции с учетом различных факторов воздействия. Важно учитывать разнообразные параметры, влияющие на численность и поведение бродячих собак в городской среде .
3.1. Уравнение размножения
Первым шагом является учет размножения собак. Это уравнение зависит от нескольких факторов, таких как возраст первого размножения, частота размножения и количество потомства. Можно использовать следующее уравнение для описания этого процесса:
где:
N – численность популяции бродячих собак,
r – скорость размножения,
K – максимальная вместимость среды.
3.2. Уравнение смертности
Смертность включает естественную смертность, болезни и травмы. Это уравнение может быть представлено как:
где:
d – коэффициент смертности.
3.3. Уравнение миграции
Если предположить, что бродячие собаки могут перемещаться в пределах города, уравнение миграции может быть включено:
где:
m – коэффициент миграции,
Nвнутри – численность популяции внутри города,
Nснаружи – численность популяции снаружи города.
3.4. Уравнение стерилизации
Эффективность программы стерилизации также должна быть учтена:
где:
s – коэффициент эффективности стерилизации.
Интегрирование этих уравнений позволяет моделировать динамику популяции бродячих собак с учетом влияния различных факторов. Модель может быть дополнена данными из реальных исследований и адаптирована под конкретные условия города. Важно регулярно обновлять параметры модели, основываясь на новых данных и изменениях в программе управления популяцией.
Давайте создадим простую модель динамики популяции бродячих собак с учетом программы стерилизации. Предположим, что стерилизация приводит к снижению рождаемости и увеличивает коэффициент смертности. Необходимо использовать логистическое уравнение для описания роста популяции с учетом стерилизации:
где:
N – численность популяции бродячих собак,
r – коэффициент размножения,
K – максимальная вместимость среды,
s – коэффициент эффективности стерилизации.
Давайте промоделируем это уравнение в течение нескольких временных шагов, чтобы увидеть, как численность популяции изменяется с течением времени в python.
import matplotlib.pyplot as plt
import numpy as np
# Параметры модели
r = 0.1 # коэффициент размножения
K = 1000 # максимальная вместимость среды
s = 0.02 # коэффициент эффективности стерилизации
# Начальные условия
N0 = 100 # начальная численность популяции
time_steps = 100 # количество временных шагов
# Массивы для сохранения данных
population = np.zeros(time_steps)
time = np.arange(0, time_steps, 1)
# Промоделируем динамику популяции
for t in range(time_steps):
dN_dt = r * N0 * (1 - N0 / K) - s * N0
N0 += dN_dt
population[t] = N0 if N0 > 0 else 0 # Ограничим численность популяции нулем
# Построим график динамики популяции
plt.plot(time, population, label='Популяция бродячих собак')
plt.xlabel('Время')
plt.ylabel('Численность популяции')
plt.title('Динамика популяции бродячих собак с учетом стерилизации')
plt.legend()
plt.show()
Этот код создает график, отражающий изменение численности популяции бродячих собак в течение времени с учетом стерилизации. Параметры модели (коэффициент размножения, максимальная вместимость среды и коэффициент стерилизации) могут быть адаптированы в зависимости от конкретных условий исследуемого города.
График, отражающий изменение численности популяции бродячих собак в течение времени с учетом стерилизации, представлен на рисунке 1.
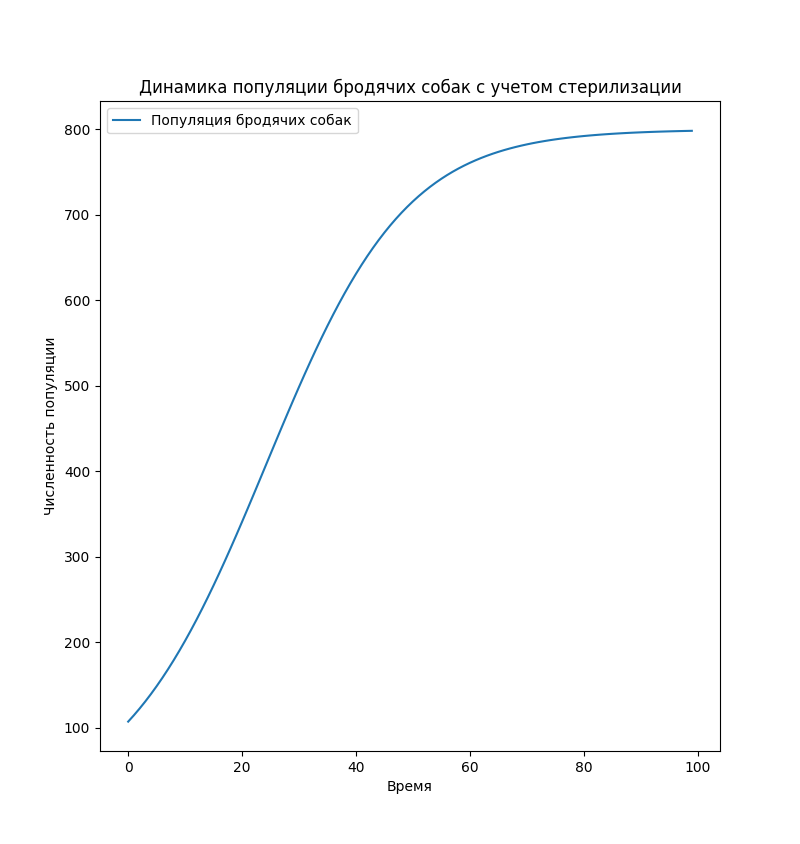
Рисунок 1 - График динамики популяции бродячих собак с учетом стерилизации
Изначально, при старте модели, численность популяции бродячих собак растет, так как коэффициент размножения r преобладает.
С увеличением численности популяции, увеличивается влияние коэффициента стерилизации s, что приводит к снижению темпов роста популяции .
После некоторого времени, при достижении максимальной вместимости среды K, рост популяции замедляется и стабилизируется.
Кривая отражает динамику управления популяцией с использованием стерилизации, позволяя достичь устойчивой и контролируемой численности бродячих собак.
4. Заключение
В заключение, математическая модель управления численностью бродячих собак при стерилизации в крупных городах представляет собой мощный инструмент для прогнозирования и оптимизации действий. В работе предложена и разработана математическая модель, описывающая динамику популяции бродячих собак с учетом различных факторов, включая размножение, смертность, миграцию и эффективность программ стерилизации.
